Kepler's Laws of Planetary Motion

Kepler's Laws of Planetary Motion

Achyut Bharadwaj
January 2020
Kepler, planetary motion, angular displacement, angular velocity, centripetal force

In this article, we will be going through some of the basic concepts required to understand Kepler’s laws.

Angular Displacement and Velocity #

Angular Displacement #

Just as displacement is defined as the change in position of an object, angular displacement is defined as the angle swept by an object travelling in a circular path.

Let’s look at an example. Say, an object travels from point $A$ to point $B$. In this process, say it covers an angle of $\theta$ (see Fig. 1)

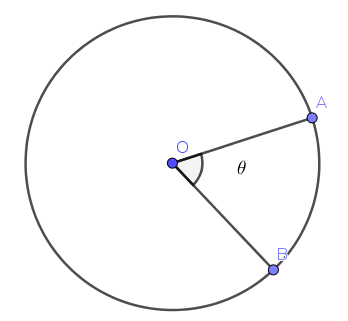
Angular displacement of object moving from $A$ to $B$
Fig-1: Angular displacement of object moving from $A$ to $B$

Here, arc $\overgroup{AB}$ is the tangential displacement and $\theta$ is the angular displacement. In this case,

(1) $$\overgroup{AB}=r\theta,$$
where $r$ is the radius of the circular path. Hence, the relationship between angular displacement and tangential displacement is:
(2) $$s=r\theta,$$
where $s$ is the tangential displacement and $\theta$ is the angular displacement.

Angular Velocity #

Just as tangential velocity is displacement per unit time, angular velocity is the angle swept per unit time. So, the average angular velocity can be written as:

(3) $$\omega_{avg}=\frac{\Delta \theta}{\Delta t},$$
where $\omega$ is the angular velocity, $\theta$ the angle swept and $t$ the time taken.

Now, as the change in time approaches 0, $\frac{\Delta \omega}{\Delta t}$ will become the instantaneous angular velocity. Angular velocity as change in time approaches 0(instantaneous angular velocity) can be represented as:

(4) $$\omega=\frac{d\theta}{dt}.$$
Note that the $d$ before $\theta$ and $t$ is just a way to represent the angular velocity as the change in time approaches 0. In general, $d$ is put before a variable to represent extremely small quantities 1.

The relationship between angular velocity and tangential velocity is:

(5) $$v=r\omega$$
where $\omega$ is the angular velocity, $v$ is the tangential velocity and $r$ is the radius of the circular path 2. We can also write the relationship as:
(6) $$\omega=\frac{v}{r}.$$

Centripetal Force #

Centripetal force is the force that acts on a body travelling in a circular path, towards the center of the circle. The numerical value of centripetal force is given by:

(7) $$F_c=\frac{mv^2}{r},$$
where $F_c$ is the centripetal force, $m$ is the mass of the body, $r$ is the radius of the path and $v$ is the tangential velocity of the body.

Now, let’s say that a person is twirling a ball of mass $m$ attached to a light and inextensible string of length $r$. Let us draw all the actual forces acting on it(ignore gravity).

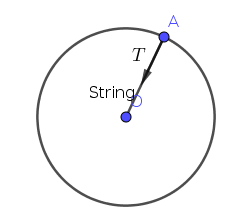
Forces acting on a twirling ball
Fig-2: Forces acting on a twirling ball

The only apparent force that is present is the tension due to the string $(T)$(See Fig. 2). But, we know that there is a centripetal force acting on any body going around in a circular path. So, we can conclude that in this case, the tension due to the string is the cause of the centripetal force. Hence, $T=F_c$.

From this, we can generically conclude that the net external force acting on a body travelling in a circular path, towards the center of the circular path is equal to the centripetal force.

Now, let us apply this to something different: Gravity.

Orbital Velocity #

Let’s start with a few problems.

A person is twirling a ball of mass $m$ attached to a light, inextensible string of length $r$ in space. Given that the tension in the string is $T$ N, find the tangential velocity.

A satellite of mass $m$ is revolving at a distance of $r$ from the center of a planet of mass $M$. Find the satellite’s tangential velocity.

If you could do the second problem on your own, you have figured out what this section is all about!

Summary #

  • The relationship between angular velocity and tangential velocity is given by:

    (8) $$\omega=\frac{v}{r},$$
    where $\omega$ is the angular velocity, $v$ the tangential velocity and $r$ the radius of the circular path.

  • Centripetal Force is given by:

    (9) $$F_c=\frac{mv^2}{r},$$
    where $F_c$ is the centripetal force, $m$ the mass of the object and $v$ the tangential velocity.

  • The Orbital velocity of a satellite of mass $m$at a distance $r$ from the center of a planet of mass $M$ is given by:

    (10) $$v_{\text{orbital}}=\sqrt{\frac{GM}{r}}.$$

Kepler’s Laws #

In this section, we will be exploring Kepler’s laws of planetary motion. Johannes Kepler was a 16th century astronomer who established three laws which govern the motion of planets (around the sun). These are known as Kepler’s law of planetary motion. The same laws also describe the motion of satellites (like the moon) around plants (like the earth).

Kepler’s First Law #

Law Statement #

Kepler’s first law states that all planets go around the Sun in an elliptical orbit, and that the Sun is at one of the foci of the orbit.

But, to understand this, we must first understand what an ellipse is.

Definition of Ellipse #

Let us first plot two points on a graph, and call it $F_1$ and $F_2$. Now, find a point which is say, a distance $r_1$ away from $F_1$, and a distance of $r_2$ away from $F_2$. Can you also find another point that is a distance $s_1$ away from $F_1$ and $s_2$ away from $F_2$, where

(11) $$r_1+r_2=s_1+s_2?$$
Now, if you plot infinite points such that
(12) $$r_1+r_2=s_1+s_2=p_1+p_2\cdots,$$
where $r_1, s_1, p_1, \dots$ are the distances of the points from $F_1$ and $r_2,s_2,p_2,\dots$ are the distances from $F_2$, what will you get? For the answer, see Fig. 3

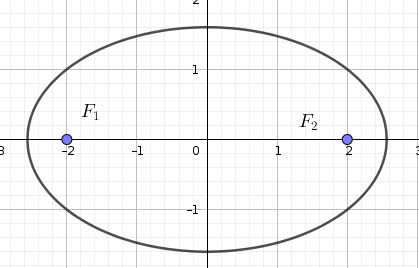
Salient points on an ellipse
Fig-3: Salient points on an ellipse

You will get an ellipse! So, An ellipse is a plane curve surrounding two focal points, such that for all points on the curve the sum of the distances to the focal points is constant, just like how all the points in a circle is equidistant from its center.

In fact both circle and ellipse are conic sections that is a curve obtained from the intersection of a cone and a plane, along with parabola and hyperbola (See Fig. 4).

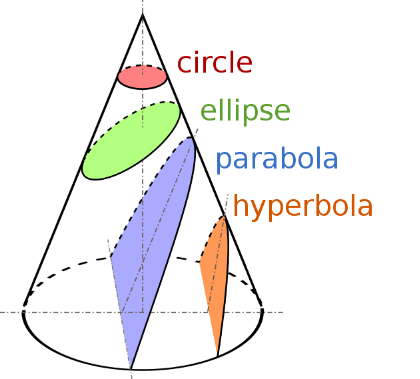
The ellipse as a conic section
Fig-4: The ellipse as a conic section

Now, it’s easier to understand what Kepler’s first law means. There is a proof for Kepler’s first law, but we are not going to prove it here.

In fact, Kepler didn’t prove this law either. He concluded that planets revolve around the Sun in elliptical orbits based on observations. It was Newton who later proved Kepler’s laws using his laws of gravitation.

Let’s move on to the second law.

Kepler’s Second Law #

Law Statement #

Kepler’s second law states that a planet moving around the sun sweeps across equal areas in equal amounts of time.

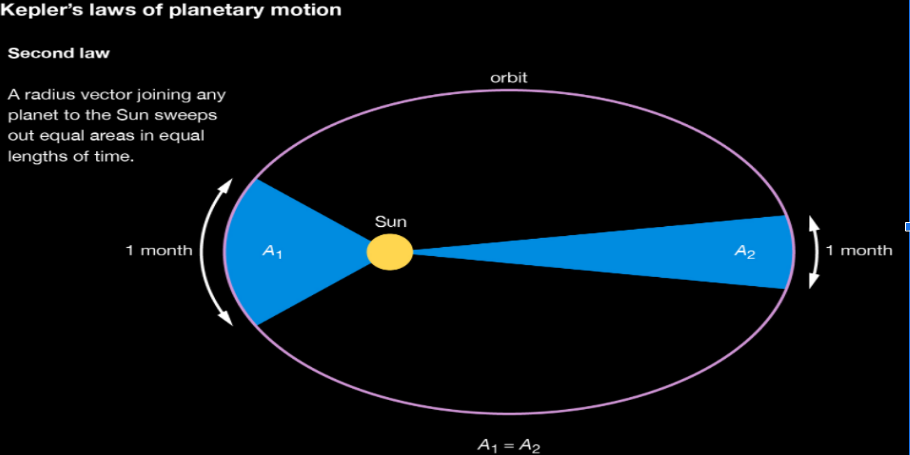
Area swept by a body in an elliptical path
Fig-5: Area swept by a body in an elliptical path

A Relation Between Distance from Planet and Velocity #

Let’s examine this closely. Just like velocity is defined as the displacement per unit time, we can define areal velocity as the area swept per unit time. We know that

(13) $$v_{\text{avg}}=\frac{\Delta s}{\Delta t},$$
where $\Delta s$ is the change in displacement and $\Delta t$ is the change in time.

So, we can say:

(14) $$\begin{aligned} \text{Areal velocity}_\text{avg} = \frac{\Delta A}{\Delta t},\end{aligned}$$
where $A$ is the area. What happens when $\Delta t$ approaches $0$? As $\Delta t$ approaches 0, the right hand side of Eqn. 14 becomes the instantaneous areal velocity instead of the average areal velocity.

So, another way to represent Eqn. 14 when $\Delta t$ approaches 0, is:

(15) $$\begin{aligned} v_A=\frac{dA}{dt},\end{aligned}$$
where $v_A$ is the instantaneous areal velocity. Now, there is no need to get scared of this. It is just a way to represent the areal velocity as the change in time approaches 0.

Now, let us take a small portion of the ellipse, where the angle made by the line segments($l_1,l_2$) which extend till the periphery of the ellipse (see Fig. 6)is $d\theta$ (Note that the $d$ before the $\theta$ represents the fact that $d\theta$ is very small).

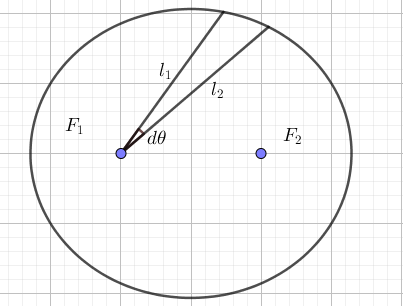
Area swept by a body in an elliptical path
Fig-6: Area swept by a body in an elliptical path

Since the angle is very small, the length of the $l_1,l_2$ are equal. Hence, we can treat the section of the ellipse as the section of a circle with center $F_1$ and radius $r$, where

(16) $$r=\text{ length of }l_1=\text{ length of }l_2.$$
Now, what is the area of this section? Well, it is simply the area of the section of a circle with radius $r$ making an angle of $d\theta$.

In general, how do we find the area of a section of a circle given that the radius is say, $s$, and the angle it makes at the center is say, $\alpha^{\circ}$?

The area will be:

(17) $$(\pi s^2)\times \frac{\alpha}{360}.$$
But, now let us say that the angle is $\beta$ radians. Radians is the SI unit for angles. $2\pi$ radians is equal to $360^{\circ}.$ Hence, if the angle is $\beta$ in radians, the area will be:
(18) $$\frac{\beta}{2\pi}\pi s^2.$$

We can apply this to the section of our ellipse, which we are treating as a section of a circle too. We know that the radius is $r$, and angle $d\theta$. So, the area($dA$) of the section can be written as:

(19) $$\begin{aligned} dA=\frac{d\theta}{2\pi}\pi r^2=r^2\frac{d\theta}{2}.\end{aligned}$$

Plugging this into Eqn. 15, we get:

(20) $$v_A=\frac{r^2\frac{d\theta}{2}}{dt}=\frac{r^2}{2}\frac{d\theta}{dt}.$$
Since we know that $\omega=\frac{d\theta}{dt}$, (Refer to Sec. 2.2) we can rewrite the above as:
(21) $$v_A=\omega\frac{r^2}{2}.$$
Since we know that $\omega=\frac{v}{r}$, we can rewrite the equation as:
(22) $$v_A=\frac{r^2}{2}\frac{v}{r}=\frac{vr}{2}.$$
Since $v_A$ is constant, we can write:
(23) $$\begin{aligned} &\frac{vr}{2}=k \implies &\boxed{vr=2k=c},\end{aligned}$$
where $k$ and $c$ are constants, and $c=2k.$ Hence, $v$ is inversely proportional to $r$, where $r$ is the distance between the planet and the Sun.

Kepler’s Third Law #

Law Statement #

Kepler’s third law states that the cube of the major axis of the orbit of a planet around the sun is directly proportional to the square of time it takes to move around the sun. The law can be expressed as:

(24) $$\begin{aligned} &T^2\propto a^3 \implies &T^2 = k\cdot a^3,\end{aligned}$$
Where $a =$ major axis of the planet’s orbit around the sun, $T =$ time period of the planet (around the sun) and $k$ is a constant.

A Little More About Ellipses #

Now, what is the major axis? It is the distance between the center of an ellipse and farthest point from the center of the ellipse(See Fig. 7).

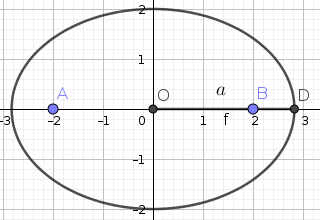
The major axis of an ellipse $\left(\overline{OD}\right)$
Fig-7: The major axis of an ellipse $\left(\overline{OD}\right)$

In Fig. 7, $a=\overline{OD}$ is the major axis.

Derivation for Circular Orbits #

Let’s now try to derive the law(for circular orbits only). First, what is time period mathematically, for circular orbits? Time period is the time an object takes to complete a full circle. In other words, it is the time takes for the object to travel a distance of $2\pi r$ units(Circumference of a circle).

Now, consider a planet travelling at a tangential velocity $v$ in a circular path with radius $r$ around the Sun. The time period will be the time taken to travel a distance of $2\pi r$. Hence, we can say:

(25) $$\begin{aligned} T=\frac{2\pi r}{v}.\end{aligned}$$
Since we know that the tangential velocity of an object in orbit at a distance $R$ from the center of a planet of mass $M$ is given by
(26) $$v_{\text{tangential}}=\sqrt{\frac{GM}{R}},$$
we can substitute
(27) $$v=\sqrt{\frac{GM}{r}},$$
where $M$ is the mass of the Sun, into Eqn. 25. Doing so, we get:
(28) $$ \begin{aligned} T &= \frac{2\pi r}{\sqrt{\frac{GM}{r}}} = \frac{2\pi r\sqrt{r}}{\sqrt{GM}} = 2\pi\sqrt{\frac{r^3}{GM}} \end{aligned}$$
Now, squaring both sides of Eqn. 28, we get:
(29) $$T^2=4\pi^2\frac{r^3}{GM}=\frac{4\pi^2}{GM}r^3.$$
Since $\frac{4\pi^2}{GM}$ is a constant, we let $k=\frac{4\pi^2}{GM}$. Hence,
(30) $$T^2=kr^3,$$
or
(31) $$\boxed{T^2\propto r^3}.$$

Summary #

  • Johannes Kepler was a 16th century astronomer who established three laws which govern the motion of planets (around the sun). These are known as Kepler’s law of planetary motion. The same laws also describe the motion of satellites (like the moon) around plants (like the earth).

  • Though Kepler gave the laws of planetary motion, he could not give a theory to explain the motion of planets. It was Newton who showed that the cause of the motion of planets is the gravitational force which the sun exerts on them. In fact, Newton used the Kepler’s third law of planetary motion to develop the law of universal gravitation.

  • Kepler’s first law #

    The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit. 

  • Kepler’s second law #

    Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time.

  • Kepler’s third law #

    The cube of the length of the major axis of the orbit of the planet around the sun is directly proportional to the square of time it takes to move around the sun (Time period). The law can be expressed as:

    (32) $$T^2\propto a^3,$$
    or
    (33) $$T^2=k\cdot a^3,$$
    where $k$ is a constant, $a =$ major axis of the orbit of the planet around the sun and $T =$time period of the planet (around the sun). 

Problems #

In this section, we are going to be exploring some problems based on what has been covered in this presentation. Note that all the problems have been framed and solved by at least one of the authors. Any problems that are not framed by the authors or any solutions that aren’t written by the authors will have their sources cited.

Problems #

Let us start with some problems. The solutions to the problems can be found in Sec. 13.

Based on Sec. 1 #

Given that the mass of the Earth is $M$ and the mass of a satellite orbiting the Earth is $m$, find the tangential velocity of the satellite given that it is orbiting the Earth in a circular path at a distance of $r$ from the center of the Earth.

A geocentric satellite is orbiting the Earth in a circular path (A geocentric satellite is a satellite that is fixed over a certain position on the Earth). Given that the mass of the Earth is $M$, the time period of the Earth is $T$ and the radius of the Earth is $R$, find:

  1. The tangential velocity of the satellite.

  2. The height (from the surface) at which the satellite orbits the Earth,

Given that the mass of the Earth is $M$, the radius of the Earth is $R$ and that the duration of a day is $T$ seconds, find the tangential velocity of an object on the surface of the Earth at the equator.

Based on Sec. 2 #

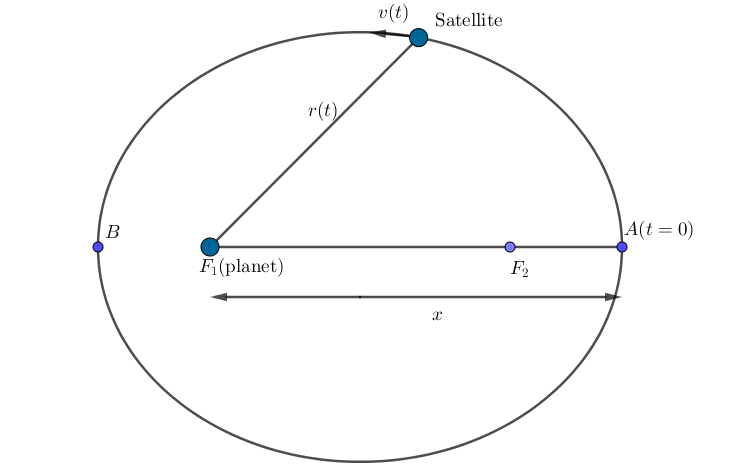
A satellite of mass $m$ is orbiting a planet of mass $M$ in an elliptical orbit such that it’s velocity as a function of time between point $A$ and point $B$ (See Fig. 8) is given by

(34) $$v(t)=t^2+23t+2.$$
Given that the distance between the planet and the satellite at point $A$ is $x$, and that $t=0$ when the satellite is at point $A$, find the distance between the planet and the satellite ($r$) as a function of time.

Satellite orbiting planet
Fig-8: Satellite orbiting planet

A satellite takes $T_1$ seconds to orbit the Earth in a circular orbit at a distance $r_1$ from the center of the Earth. If another satellite is orbiting the Earth in a circular orbit at a distance $r_2$ from the center of the Earth, find the time period of the satellite orbiting at the height $r_2-R$, where $R$ is the radius of the Earth.

A satellite takes $T_1$ seconds to orbit the Earth in a circular orbit at a distance $r_1$ from the center of the Earth. If another satellite orbiting the Earth in a circular orbit takes $T_2$ seconds to come back to the same position with respect to the Earth, find the height at which it orbits assuming that the direction of revolution of both satellites are in the same direction as the rotation of the Earth. (Take the duration of a day as $T$ seconds).

Solutions #

Here are the solutions to the problems from Sec. 12.

Solutions to Problems Based on Sec. 1 #

We have already seen that

(35) $$v_{\text{orbital}}=\sqrt{\frac{GM}{r}},$$
where $v_{\text{orbital}}$ is the tangential velocity of orbital of a satellite around a planet, $M$ the mass of the planet and $r$ the radius of the orbit (Refer to Sec. 4).

Directly applying this to the problem, we get

(36) $$\boxed{v=\sqrt{\frac{GM}{r}}}.$$

[[sol.1]]{#sol.1 label=“sol.1”} The time period of an object going in a circular path with a tangential velocity say $v$ is given by:

(37) $$T=\frac{2\pi r}{v},$$
where $T$ is the time period, and $r$ the radius of the circular path.(Time period is distance covered divided by velocity, and the distance in a circular path is $2\pi r$).

Now, let’s come back to the problem.

Let $v$ be the tangential velocity and $r$ be the distance between the satellite and the center of the Earth.

Part (a) #

The tangential velocity will be:

(38) $$\begin{aligned} {v=\sqrt{\frac{GM}{r}}}.\end{aligned}$$
Applying the formula for time period, we get:
(39) $$ \begin{aligned} &T=\frac{2\pi r}{v} \implies & r=\frac{Tv}{2\pi} \end{aligned}$$
Substituting $v=\sqrt{\frac{GM}{r}}$ from Eqn. 38 into Eqn. 39, we get:
(40) $$ \begin{aligned} &r=\frac{T\sqrt{\frac{GM}{r}}}{2\pi} \implies &r\sqrt{r}=\sqrt{r^3}={T\frac{\sqrt{GM}}{2\pi}} \implies & r=\sqrt[3]{\frac{T^2GM}{4\pi^2}} \end{aligned}$$
(41) $$\begin{aligned} \implies & r-R=\text{height from surface}=\boxed{\sqrt[3]{\frac{T^2GM}{4\pi^2}}-R}. \end{aligned}$$

Part (b) #

Substituting the result we got for $r$ in Eqn. 40, into Eqn. 38, we get:

(42) $$v={\sqrt{\frac{GM}{\sqrt[3]{\frac{T^2GM}{4\pi^2}}}}}=\boxed{\sqrt[3]{\frac{2\pi GM}{T}}}.$$

We know that

(43) $$\begin{aligned} T=\frac{2\pi R}{v}, \end{aligned}$$
where $v$ is the velocity of an object on the surface of the Earth. Dividing both sides of Eqn. 43 by $T$ and multiplying both sides of it by $v$, we get:
(44) $$v=\boxed{\frac{2\pi R}{T}}$$

Solutions to Problems Based on Sec. 2 #

We have seen that the areal velocity of a satellite in an elliptical orbit is:

(45) $$v_A=\frac{vr}{2},$$
where $v_A$ is the areal velocity, $v$ the tangential velocity at a point and $r$ the distance between the point and the planet(Refer to Sec. 8.2).

Letting areal velocity be $v_A$ and applying the concept to this problem, we get:

(46) $$\begin{aligned} v_A=\frac{v(t)r(t)}{2} \end{aligned}$$
But, what is $v_A$? How do we find it?

Since $v_A$ is constant by Kepler’s third law, $v_A$ at $t=0$ will be the same as the $v_A$ in Eqn. 34. We can easily find both $v(0)$ and $r(0)$. So, we can simply substitute $t=0$ in Eqn. 34 to find the areal velocity.

Substituting $t=0$ in the function $v(t)$, we get:

(47) $$v(0)=0^2+23\times 0 +2 = 2.$$
We are also given that the distance between point $A$ and the planet is $x$(Refer to Fig. 8) and that $t=0$ at point $A$. So, $r(0)=x.$ Hence,
(48) $$v_A=\frac{2x}{2}=x.$$
Substituting $v_A=x$ in Eqn. 46, we get:
(49) $$\begin{aligned} &x=\frac{v(t)r(t)}{2} \implies &v(t)r(t)=2x \implies &r(t)=\frac{2x}{v(t)}=\boxed{\frac{2x}{t^2+23t+2}}. \end{aligned}$$

[[sol.2]]{#sol.2 label=“sol.2”} Using Kepler’s third law, we can say that (Refer to Sec. 9):

(50) $$T_1^2 \propto r_1^3,$$
or
(51) $$ \begin{aligned} &T_1^2=kr_1^3 \implies &k=\frac{T_1^2}{r_1^3}, \end{aligned}$$
where $k$ is a constant.

Now, we let the time period of the other satellite be $T_2$. Hence, we can say that:

(52) $$T_2^2\propto r_2^3,$$
or
(53) $$\begin{aligned} T_{2}^{2}=kr_2^3 \end{aligned}$$
Substituting $k$ from Eqn. 51 into Eqn. 53, we get:
(54) $$T_2^2=\frac{T_1^2}{r_1^3}\cdot r_2^3.$$
Taking the square root on both sides, we get:
(55) $$T_2=\boxed{T_1\sqrt{\left(\frac{r_2}{r_1}\right)^3}}.$$

Let $r_2$ be the distance from the center of the Earth that the satellite revolves.

So, we know that:

(56) $$ \begin{aligned} &T_1^2=kr_1^3 \implies & k=\frac{T_1^2}{r_1^3}, \end{aligned}$$
where $k$ is a constant.

You might be tempted to do the same as in solution [sol.2]{reference-type=“ref” reference=“sol.2”}, but we haven’t found the time period of the second satellite, since we are only given the time period of the second satellite with respect to the Earth and not the time period of the satellite with respect to space. So, we need to find it’s time period with respect to space.

Since we are given that the satellite revolves in the same direction as the Earth’s rotation, we can simply add the time period of the Earth and the time period of the satellite with respect to the Earth to get the satellite’s time period with respect to space. Hence,

(57) $$T_2'=T+T_2,$$
where $T_2’$ is the actual time period of the satellite.

Hence, by Kepler’s third law,

(58) $$ \begin{aligned} &T_2'^2=kr_2^3 \implies & r_2=\sqrt[3]{\frac{T_2'^2}{k}}. \end{aligned}$$
Now, substituting what we got for $k$ in Eqn. 56 into Eqn. 58, we get:
(59) $$\begin{aligned} r_2=r_1\sqrt[3]{\frac{T_2'^2}{T_1^2}}. \end{aligned}$$
Substituting $T_2’=T+T_2$, and into Eqn. 59, we get:
(60) $$\begin{aligned} r_2=r_1\sqrt[3]{\left(\frac{T+T_2}{T_1}\right)^2}. \end{aligned}$$
Since we took $r_2$ as distance from center of the Earth, $r_2=R+h$, where $h$ is the height from the surface of the Earth.

Substituting $r_2=R+h$ into Eqn. 60, we get:

(61) $$\begin{aligned} & R+h=r_1\sqrt[3]{\left(\frac{T+T_2}{T_1}\right)^2} \implies & h=\boxed{r_1\sqrt[3]{\left(\frac{T+T_2}{T_1}\right)^2}-R}. \end{aligned}$$

  1. This symbol is extensively used in calculus where to denote the slope of the tangent to a curve at a particular point ↩︎

  2. This can easily be derived from the fact that $s=r\theta$ and that $v=\frac{ds}{dt}$}, ↩︎