Achyut Bharadwaj, Saee Patil, Valentio Iverson, Danny Li August 2021 Acknowledgements
# This work was carried out as part of a research project at PROMYS-2021 . I am a grateful recipient of the Mehta Fellowship to the PROMYS programs in 2021 and 2022.
Preliminary Definitions
# Finding Patterns
# (1) $$1,4,7,10,\cdots\;\;?$$
Here’s a harder one:
(2) $$3,4,6,9,13,\cdots\;\;?$$
Notations
# (3) $$\Delta\left(f\right)(x)=f(x+1)-f(x)$$
(4) $$\Delta^{n+1}(f)=\Delta\left(\Delta^n(f)\right)$$
What is $\Delta\left(f\right)$ when $f$ is $1,4,7,10,\cdots$?
What is $\Delta\left(f\right)$ when $f$ is $3,4,6,9,13\cdots$?
What is $\Delta^2(f)$ when $f$ is $3,4,6,9,13\cdots$?
Some Results
# $\Delta\left(f\right)$ is a polynomial iff $f$ is a polynomial.
(5) $$\Delta^n(f)=c\Rightarrow \Delta^{n+1}(f)=0$$
Let
(6) $$f(x)=a_mx^m+a_{m-1}x^{m-1}+\cdots+a_1x+a_0,a_m\neq0$$
The least $n$ such that $\Delta^n(f)=0$ is $m+1$.$\Delta^{-1}$
# We define $\Delta^{-1}(f(x))$ as a function $g(x)$ such
that $\Delta\left(g(x)\right) = f(x)$.
Patterns again!
#
(7) $$1^2 + 2^2 + 3^2 + \cdots + (n-1)^2 = ~?$$
What about(8) $$1^3 + 2^3 + \cdots + (n-1)^3 = ~?$$
Can you find(9) $$\sum_{i=0}^{n-1} i^k$$
recursively?Generalizing
# Observe that
(10) $$\sum_{i=0}^{n-1}(i+1)^k - \sum_{i=0}^{n-1}i^k = n^k$$
So,(11) $$\sum_{i=0}^{n-1}(i+1)^k - i^k = n^k$$
The above becomes:
(12) $$\sum_{i=0}^{n-1}\sum_{j=1}^{k}\binom{k}{j}i^{k-j} = \sum_{i=0}^{n-1}(ki^{k-1} + \sum_{j=2}^{k}\binom{k}{j}i^{k-j}) = n^k$$
using the binomial theorem.So, we have
(13) $$n^k-\sum_{i=0}^{n-1}(\sum_{j=2}^{k}\binom{k}{j}i^{k-j}) = k\sum_{i=0}^{n-1}i^{k}$$
by rearranging the above.Hence,
(14) $$\sum_{i=0}^{n-1}i^k = \frac{n^k - \sum_{i=0}^{n-1}(\sum_{j=2}^{k}(\binom{k}{j}i^{k-j}))}{k}$$
Calculus vs Finite Differences
# Addition and multiplication under a finite difference
# (15) $$\Delta\left(f(x)+g(x)\right) = \Delta\left(f(x)\right)+\Delta\left(g(x)\right)$$
(16) $$\begin{aligned}\Delta\left(f(x)+g(x)\right) &= (f(x+1)+g(x+1)) - (f(x)+g(x)) \\ &= (f(x+1)-f(x)) + g(x+1) - g(x) \\ &= \Delta\left(f(x)\right) + \Delta\left(g(x)\right)\end{aligned}$$
Multiplication of finite difference
# We now try to find a generic formula
for the product of two functions under a finite difference.
(17) $$\Delta\left(f(x)\cdot g(x)\right) = f(x+1)\Delta\left(g(x)\right) + g(x)\Delta\left(f(x)\right)$$
(18) $$\Delta\left(f(x)\cdot g(x)\right) = f(x+1)g(x+1) - f(x)g(x)$$
We add and subtract $g(x)f(x+1)$ in the above to get:(19) $$\begin{aligned} \Delta\left(f\cdot g\right) &= f(x+1)g(x+1) - f(x)g(x) + f(x+1)g(x) - f(x+1)g(x) \\ &= f(x+1)(g(x+1) - g(x)) + g(x)(f(x+1)-f(x)) \\ &= f(x+1)\Delta\left(g(x)\right) + g(x)\Delta\left(f(x)\right) \end{aligned}$$
Division under a finite difference
# Before trying to find a formula for
division, we try to find one for the multiplicative inverse, i.e.
finding $\Delta\left(\frac{1}{f(x)}\right)$ in terms of $f(x)$
(20) $$\Delta\left(\frac{1}{f(x)}\right) = \frac{1}{f(x+1)} - \frac{1}{f(x)} = \frac{f(x)-f(x+1)}{f(x+1)f(x)} = -\frac{\Delta\left(f(x)\right)}{f(x+1)f(x)}$$
Now,(21) $$\Delta\left(\frac{f(x)}{g(x)}\right) = \Delta\left(f(x)\cdot\frac{1}{g(x)}\right) = f(x+1)\Delta\left(\frac{1}{g(x)}\right) + \frac{1}{g(x)}\Delta\left(f(x)\right)$$
by the product formula.
The above can be written as:(22) $$-f(x+1)\frac{\Delta\left(g(x)\right)}{g(x+1)g(x)} + \frac{\Delta\left(f(x)\right)}{g(x)} = \frac{g(x+1)\Delta\left(f(x)\right)-f(x+1)\Delta\left(g(x)\right)}{g(x+1)g(x)}$$
Chain Rule
# Evaluate $\Delta\left(f(x)\right)$ when $f(x)=(2x)^2$
$(2x)^2 = 4x^2$. Now, $\Delta\left(4x^2\right) = 4\Delta\left(x^2\right) = 4(2x+1) = 8x+4$.
We compare this with the calculus chain rule. Is it possible to let
$u=2x$, find $\Delta\left(f(u)\right)$, and multiply it by $\Delta u$ to get the
result as we do in calculus?
(23) $$f(u)=u^2 \implies \Delta f(u) = 2u + 1 = 4x + 1$$
Also, $\Delta u = 2$.
So,(24) $$\Delta f(u)\cdot \Delta u = (4x+1)\times2 = 8x + 2 \neq 8x+4$$
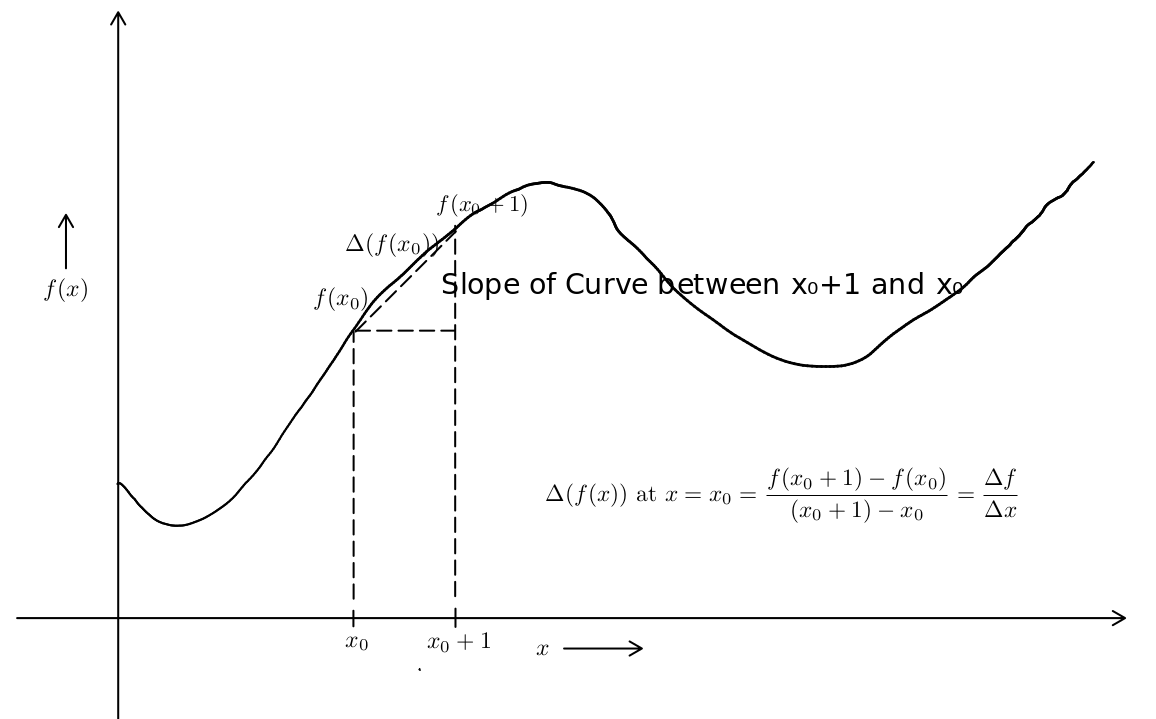
We
explore why it does not work in the next few slides.We think of the function $\Delta$ as finding the slope of a
curve between two integral points.
Fig-1:
Chain Rule So, we can conclude that
(25) $$\Delta\left((f)(x)\right) = \frac{\Delta\left(f(x)\right)}{\Delta x}$$
We need
(26) $$\frac{\Delta f}{\Delta g}\cdot\frac{\Delta g}{\Delta x} = f(g(x))\Delta\left(g(x)\right)$$
for the chain rule to work.We know that
(27) $$\frac{\Delta g(x)}{\Delta x} = \Delta g(x)$$
from the graph
in Fig-1 . Hence, we need(28) $$\frac{\Delta f(x)}{\Delta g(x)} = f(g(x))$$
for the chain rule to work.
This however does not hold true for every $f(x),g(x)$ as we saw in the
example.In calculus however, the difference is not finite. Hence, the above
holds.
Some fun with $\Delta^{-1}$
# Find $\Delta^{-1}(x + 1)$. Can you find $\Delta^{-1}(f(x)+g(x))$ in
terms of $f(x),g(x)$?
We know
(29) $$\Delta^{-1}(2x+1) = x^2+c$$
. Also,(30) $$\Delta^{-1}x = \frac{x^2-x}{2}+c$$
So, one can guess that(31) $$\Delta^{-1}(2x+1) = x^2 - \frac{x^2-x}{2} = \frac{x^2 + x}{2}+c$$
for
some constant $c$. Indeed, we can check to see that this is true!
Notice that this is the same as(32) $$\Delta^{-1}(x) + \Delta^{-1}(1)$$
This
leads to a proposition.Addition under $\Delta^{-1}$
#
(33) $$\Delta^{-1}(f+g) = \Delta^{-1}(f)+\Delta^{-1}(g)$$
for all $f,g$ whose
differences are defined.We know that
(34) $$\Delta\left(f'+g'\right) = \Delta\left(f'\right)+\Delta\left(g'\right)$$
Now,(35) $$\Delta^{-1}(\Delta\left(f'+g'\right)) = f'+g'$$
Hence,(36) $$\Delta^{-1}(\Delta\left(f'\right)+\Delta\left(g'\right))=f'+g'$$
Also,
(37) $$\Delta^{-1}(\Delta\left(f'\right)) + \Delta^{-1}(\Delta\left(g'\right)) = f' + g'$$
Equating the LHS of the above two equations, we get:
(38) $$\Delta^{-1}(\Delta\left(f'\right)+\Delta\left(g'\right))=\Delta^{-1}(\Delta\left(f'\right)) + \Delta^{-1}(\Delta\left(g'\right))$$
We let(39) $$\Delta\left(f'\right) = f, \Delta\left(g'\right) = g$$
Thus,(40) $$\Delta^{-1}(f+g) = \Delta^{-1}(f)+\Delta^{-1}(g)$$
for all $f,g$ given
that $f’,g’$ exist. That is, $f$ and $g$ must have defined differences.Generalizing
# A motivating question
# We are interested in the following question.
Can we find a polynomial that fits a certain given data?
Let us consider the following example. Can we find a quadratic
polynomial $f$ such that
(41) $$f(0) = 1, f(1) = 0, f(2) = 5, f(3) = -1~?$$
A motivating question indeed, and the answer is no . Suppose there exists
such quadratic polynomial $f$, then
(42) $$\Delta^3 f(x) = 0, \forall x \in \mathbb{R}$$
However, we can check
that(43) $$\Delta^3 f(0) = f(3) - 3f(2) + 3f(1) - f(0) = -17$$
Consider a variant of the question before:
Can we find a cubic polynomial $f$ such that
(44) $$f(0) = 1, f(1) = 0, f(2) = 5, f(3) = -1~?$$
The answer is yes! The polynomial(45) $$-\frac{17}{6}x^3+\frac{23}{2}x^2 - \frac{29}{3}x + 1$$
works. But how
do we find this polynomial?Since
(46) $$\Delta\left(\Delta^2(f(x))\right) = -17$$
(47) $$\Delta^2(f(x)) = -17x + c$$
for some constant $c$. When $x=0$,(48) $$\Delta^2(f(x)) = 6$$
Hence, $c=6$. Similarly,(49) $$\Delta^2(f(x)) = -17x+6 \implies \Delta\left(f(x)\right) = -\frac{17}{2}x^2 + \frac{29}{2}x + c'$$
for some constant $c’$. When $x=0$, $\Delta\left(f(x)\right) = -1$. Hence,
$c’ = -1$. We could check that(50) $$\Delta\left(f(x)\right) = \frac{17}{2}x^2 + \frac{29}{12}x - 1$$
, which implies(51) $$f(x) = -\frac{17}{6}x^3 + \frac{23}{2}x^2 - \frac{29}{3}x + c''$$
When
$x=0$, $f(x) = 1$. Hence, $c’’=1$. Thus, the cubic polynomial that fits
the given data is(52) $$-\frac{17}{6}x^3+\frac{23}{2}x^2 - \frac{29}{3}x + 1$$
Can we generalize this? Therefore, we began to ask the following
interesting question:
Given the values of $f(0), f(1), \dots, f(n)$, can we find a polynomial
$f$ of degree not greater than $n$ that fits this data? Is this
polynomial unique?
And the answer is yes to both questions.
Finding a polynomial that passes through $n$ points
# Claim. For any
$n,k, i \le k$, we have
(53) $$\Delta^i \binom{n + k}{k} = \binom{n + k}{k - i}$$
We will prove this by induction on $i$. Indeed, this is true for
$i = 1$, since
(54) $$\Delta \binom{n + k}{k} = \binom{n +k + 1}{k} - \binom{n + k}{k} = \binom{n + k}{k - 1}$$
Now,
fix $n,k$. Suppose this result is true for $i = \ell < k$, Then we will
prove that this is true for $i = \ell + 1$.Indeed,
(55) $$\begin{aligned} \Delta^{\ell + 1} \binom{n + k}{k} &= \Delta \left( \Delta^{\ell} \binom{n + k}{k} \right) \\ &= \Delta \binom{n + k}{k - \ell} \\ &= \binom{n + 1 + k}{ k - \ell} - \binom{n + k}{k - \ell} \\ &= \binom{n + k}{k - \ell - 1} \end{aligned}$$
which proves our assertion.Every polynomial $P(x)$ can be uniquely represented as
(56) $$\sum_{k} a_k \binom{n + k}{k}$$
for reals $a_k$.Using this fact, note that if $P(x) \not= 0$, then
(57) $$\begin{aligned} \Delta^{-1}(P(x)) &= \sum_k a_k \Delta^{-1} \left( \binom{n + k}{k} \right) = \sum_k a_k \binom{n + k}{k + 1}\end{aligned}$$
The previous argument
proves the existence of such a polynomial passing through
$f(0), f(1), f(2), \dots, f(n)$, ensuring the degree is not greater than
$n$.
In fact, we claim an even more generalized result.
Let $x_1, x_2, \dots, x_n$ be $n$ distinct real values and
$y_1, y_2, \dots, y_n$ be $n$ real numbers. Then there exists a unique
polynomial $f \in \mathbb{R}[x]$ of degree less than $n$ such that
$f(x_i) = y_i$ for $1 \le i \le n$.
Proof
# Proof. We’ll first prove that there exists such polynomial.
Consider the polynomial
(58) $$f(x) = \sum_{i = 1}^n y_i \cdot \prod_{i \not= j} \frac{x - x_j}{x_i - x_j}$$
Now, check that $f(x_i) = y_i$ for every $1 \le i \le n$, and we are
done. Finally, we will prove uniqueness. Indeed, if there exists two
working polynomials $Q,R$ such that(59) $$Q(x_i) = R(x_i) = y_i$$
for
$1 \le i \le n$. Then, either $Q - R = 0$, or $\text{deg} (Q - R) < n$.
However, if $Q - R \not= 0$, the polynomial $Q - R$ vanishes at $n$
points, with degree less than $n$, which is a contradiction.