Balancing Centrifuges: Vanishing Sums of Roots of Unity
Achyut Bharadwaj, Tanmay Gupta, James Shuffelton, Toyesh Jayaswal, Matt BakerAugust 2022
Abstract #
The problem of balancing centrifuges is equivalent to finding sets of $k$ $n$-th roots of unity that sum to $0$. We can represent each slot in the centrifuge as an $n$-th root of unity as the slots in the centrifuge are also equally spaced and equidistant from the origin.
Acknowledgements #
Accepted for publication at the Joint Mathematics Meetings, Boston, January 4 – 7, 2023.
This work was carried out as part of a research project at PROMYS-2022. I am a grateful recipient of the Mehta Fellowship to the PROMYS programs in 2021 and 2022.
We would like to thank Professor Matt Baker for proposing this project and mentoring us. We also are very grateful to Toyesh Jayaswal, our counselor who consistently supported our mathematical explorations. We also thank Professor David Fried, John Sim, The Clay Mathematics Institute, and the PROMYS Program for giving us this amazing opportunity to participate in this research lab.
Introduction #
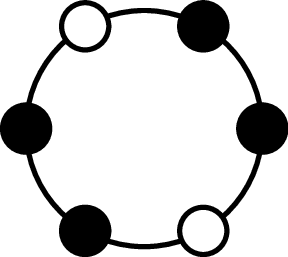
Consider a centrifuge with $n$ holes and $k$ vials that we want to place. The centrifuge’s center of mass needs to be at the center of rotation for the centrifuge to function safely. We call such a centrifuge balanced. For instance, consider the below balanced configuration for $n = 6, k = 3.$
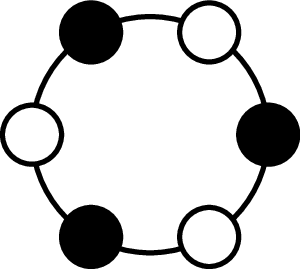
The problem of balancing centrifuges is equivalent to finding sets of $k$ $n$-th roots of unity that sum to $0$. We can represent each slot in the centrifuge as an $n$-th root of unity as the slots in the centrifuge are also equally spaced and equidistant from the origin.
Prior Work #
Sivek’s Main Theorem #
Theorem-1#
$k$ vials can be be balanced in a centrifuge with $n$ slots if and only if $k$ and $n-k$ can both be written as sum of prime factors of $n$ (Note: repetition of prime factors in sums is allowed).
Consider the following examples. For $n=12, k=8$ can be balanced because $k = 8 = 2+2+2+2$ and $n-k = 4 = 2+2.$ On the other hand, for $n=15, k=11$ cannot be balanced since even though $k=11=3+3+5,$ $n-k$ cannot be expressed as a sum of $3$’s and $5$’s.
Sivek’s proof builds upon a more general theorem:
Lam and Leung’s Main Theorem #
Theorem-2#
There exist $k$ $n$-th roots of unity that sum to zero (allowing a root to appear multiple times) if and only if $k$ is a sum of prime factors of $n.$
Definition-2#
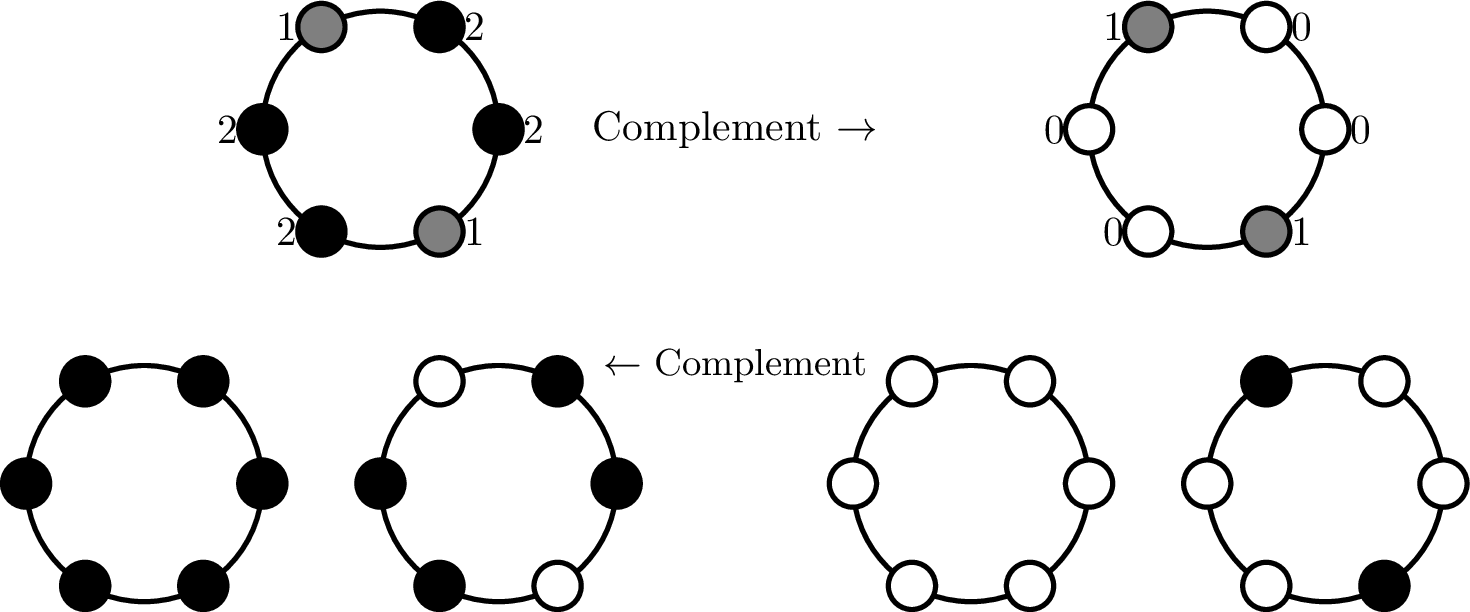
The complement of a balanced configuration of vials is obtained by placing vials in the empty spots and removing the vials from the initial configuration.For instance, the two configurations below are complements of each other.

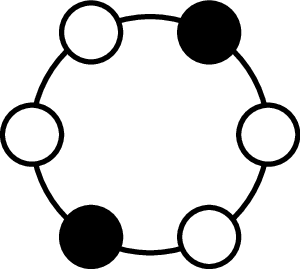

Complement Principle #
Proposition-1#
A configuration is balanced if and only if its complement is balanced. (Corollary: $k$ can be balanced if and only if $n-k$ can be balanced).
Proof: Balancing the centrifuge is equivalent to finding the $n$-th roots of unity that sum to $0$. All $n$-th roots of unity sum to zero. Thus, if we take a subset of the $n$-th roots of unity that sums to zero, the complement must also sum to zero because $0-0=0.$ $$\square$$
Sivek considers what additional restrictions are imposed when roots are restricted so that they cannot be repeated in the sum. This models a centrifuge as two vials will not be placed in the same slot. While the full proof of Sivek’s theorem can be found in [@sivek2010vanishing], we discuss the connection between the two theorems below.
Not allowing repeated roots of unity is a subset of all sums that do allow repeated roots of unity. Thus, for any balanced centrifuge, Lam and Leung’s Main Theorem shows that $k$ is a sum of prime factors of $n.$ Now, if we take the complement of a balanced centrifuge, then it will also be balanced, similarly giving us that $n-k$ is a sum of prime factors of $n.$ Thus, the condition of $k$ and $n-k$ being a sum of prime factors of $n$ for a centrifuge to be balanced is necessary due to Lam and Leung’s Main Theorem. Sivek proves that this condition is also sufficient.
One Centrifuge, Equally Massed Vials #
In order to gain a better understanding of the problem during our initial exploration, we attempted to re-prove that if $k$ and $n-k$ are sums of prime factors of $n$, then we can construct a balanced centrifuge with $k$ vials and $n$ slots (one direction of the implication in Sivek’s Main Theorem).
Consider a prime factor of $n$, say $p$. Then, we notice that the configuration with $p$ equally spaced vials is balanced due to the following: This case is equivalent to $p$ equally spaced $n$-th roots of unity starting with $1$ (WLOG). If the sum of these equally spaced $n$-th roots of unity is $0$, then the configuration is balanced. In our case, the sum is
This motivates us to build balanced configurations of $k$ vials with groups of $p_i$ equally spaced vials, where $p_i$ is a prime factor of $n.$ Note that the groups may need to be rotated to prevent two vials from overlapping at the same position. For instance, consider the diagram below of $n=12$, $k=7.$ The vials are split up into two groups of two vials and one group of three vials.
This transforms one direction of the implication into proving that such a construction with no overlaps exists.
We first deal with this problem for simpler cases.
Thus, we first consider the case when $n=p^\alpha$ for some $\alpha \in \mathbb{N}$. The only values of $k$ that are a sum of prime factors of $n$ in this case are multiples of $p$. Thus, we want to prove that if $k$ is a multiple of $p$, then we may find a configuration with $k$ vials that is balanced. Note that in this case, $n-k$ is a sum of prime factors of $n$ if and only if $k$ is a sum of prime factors of $n$, so we can ignore that condition for now.
Proposition-2#
We can balance $k$ vials in a centrifuge with $n$ slots where $n = p^{\alpha}$ for some prime $p$ if $k$ is a multiple of $p$.
Proof: For $p$ prime and $n=p^\alpha$, let $k=p\cdot x$ and $n-k=p\cdot (p^{\alpha -1}-x).$ Then, we can consider placing $x$ groups of $p$ evenly-spaced centrifuges (i.e. rotated versions of the $p$-th roots of unity). This will be balanced because the $p$-th roots of unity sum to zero, and therefore a sum of rotated $p$-th roots of unity will also sum to zero.
We want to ensure it is possible to construct such a configuration without overlaps. Note that we can label the spots in the centrifuge by indexing modulo $p^\alpha.$ Now, we can consider the $i$-th group of (potentially) rotated $p$-th roots of unity (where $0 \leq i < x$) to be placed in the indices/positions given by the equation $p^{\alpha -1}\cdot m_i+b_i \pmod{p^{\alpha}}$ where $b_i$ fixes the rotation, and $m_i$ is any integer. Now, suppose we choose $b_i=i.$ We recognize that $x\leq p^{\alpha -1}$ because $k\leq n.$ Now consider any two of the equations and set them equal to see if there will be any overlap.
Now, we consider the case when $n=pq$ where $p$ and $q$ are distinct primes. We have that $k$ and $n-k$ are both sums of prime factors of $n$ if and only if $p|k$ or $q|k$.
Proposition-3#
If $k$ and $n-k$ are both sums of prime factors of $n=pq$ for two distinct primes $pq$, then $p \mid k$ or $q \mid k.$
Proof: If $k$ and $n-k$ are both sums of prime factors of $n=pq$, then suppose $k=ap+bq$ and $n-k=cp+dq.$ So, we have $(a+c)p+(b+d)q=pq.$ So, we see that $p \mid (b+d)$ and $q \mid (a+c).$ Both $(a+c)$ and $(b+d)$ cannot be nonzero, since then $k>n.$ This means that at least one of $a=0$ or $b=0$ must be true, making at least one of $p \mid k$ or $q \mid k$ true. $$\square$$
Now, we prove that when $k$ is a multiple of either $p$ or $q$, we can balance the configuration.
Proposition-4#
We can balance $k$ vials of a centrifuge with $n$ spots where $n=pq$ for primes $p$ and $q$ when $p|k$ or $q|k$.
Proof: Suppose $p|k$ without loss of generality. Then, we have $k = px$ for some $x \in \mathbb{Z}$. In order to prove that $k$ is balanced, we must find a construction of $k$ vials that is balanced.
Notice that since $p$ equally spaced vials is a configuration that is balanced, placing $x$ sets of $p$ equally spaced vials such that no two sets overlap is also a balanced configuration.
Thus, we are only left to prove that no two sets of $p$ equally spaced vials among the $x$ sets of $p$ equally spaced vials overlap at any point.
Suppose we label the slots in the centrifuge from $0$ to $n-1$. The position of the $i$-th vial in the first group of $p$ vials is given by $qi$ (assuming without loss of generality that the first vial in this set is placed at $0$). Consider another set whose first vial is placed at position $a$. Then, the position of the $j$-th vial in this set of $p$ $n$-th roots of unity is $qj + a$. Now, consider the construction of groups of $p$-th roots of unity such that we have $a$ be each value in ${0, 1, \cdots q-1}$ once. We must thus prove that there do not exist a pair $(i, j)$ such that $qi+a_1= qj + a_2$ given any $a_1, a_2 \in {0, 1, \cdots q-1}, a_1 \neq a_2$.
Suppose for the sake of contradiction there exists a pair $(i, j)$ such that $qi +a_1\equiv qj + a_2 \pmod{n}$. Taking both sides modulo $q$, we get $a_1 \equiv a_2 \pmod{q}$. However, there is no solution to this with distinct $a_1, a_2$ since $0\leq a_1, a_2 < q$. $$\square$$
In both cases, we have that we are able to balance $k$ when $k$ is a multiple of a prime factor of $n$. This motivates the following proposition.
Proposition-5#
Consider a prime $p$ such that $p|n$. If $p|k$, we can construct a configuration with $k$ vials that is balanced. In other words, $k$ vials can be balanced in a centrifuge with $n$ slots if $(k, n)>1$.
Proof: Let $p_1, p_2, \cdots, p_z$ be prime and $n=p_1^{\alpha_1}\cdot p_2^{\alpha_2}\cdot \cdots \cdot p_z^{\alpha_z}.$ Now, let $k=p_l\cdot x$ for some $p_l \in {p_1, p_2, \cdots, p_z}.$ Then, we can consider placing $x$ groups of $p_l$ evenly spaced vials (i.e. a potentially rotated version of the $p_l$-th roots of unity). This will be balanced because the $p_l$-th roots of unity sum to zero, and therefore a sum of rotated groups of the $p_l$-th roots of unity will also sum to zero. Now, we want to make sure it is actually possible to place such a configuration. In order to do this, we want to make sure that any vials we place do not overlap with each other. Note that we can label the spots in the centrifuge by indexing modulo $n.$ Now, we can consider the $i$-th group of (potentially) rotated $p_l$-th roots of unity (where $0 \leq i < x$) to be placed in the indices/positions given by the equation $\frac{n}{p_l}\cdot m_i+b_i \pmod{n},$ where $m_i$ varies for each vial. Now, suppose we choose $b_i=i.$ We recognize that $x\leq \frac{n}{p_l}$ because $k\leq n.$ Now consider any two of the equations and set them equal to see if there will be any overlap.
Two Centrifuges #
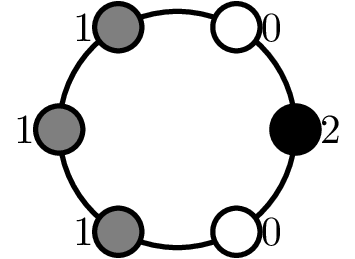
Now that we have an understanding of one centrifuge, we move to allowing for two centrifuges. Here, we have some $k$ between $0$ and $2n$ that we want to balance using two centrifuges (both are $n$-slot centrifuges). For instance, for $n=6,$ $k=7=3+4$ can be balanced over two centrifuges as shown below.
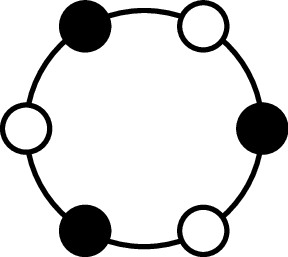

Definition-1#
For a given $n,$ we say $k$ is $2$-centrifuge admissible if we can balance $k$ vials over two $n$-slot centrifuges. More generally, we say $k$ is $r$-centrifuge admissible if we can balance $k$ vials over $r$ $n$-slot centrifuges.
Proposition-6#
$k$ is $2$ centrifuge admissible if and only if there exist $k_1, k_2$ that are $1$ centrifuge admissible such that $k = k_1 + k_2$.
Proof: Any $k$ that can be balanced over two centrifuges is split into $k = k_1 + k_2,$ where we balance $k_1$ vials in the first centrifuge, followed by $k_2$ vials in the second centrifuge. $k_1$ and $k_2$ each have to be balanced over $n$ spots. The converse is also true: if $k_1$ and $k_2$ are $1$-centrifuge admissible, then the sum $k = k_1+k_2$ can be balanced with two centrifuges with $k_1$ vials in the first centrifuge and $k_2$ in the second. As discussed, in Section [3](#sec: one round){reference-type=“ref” reference=“sec: one round”}, this happens if and only if $k_1, k_2, n-k_1,\text{ and } n-k_2$ can be expressed as a sum of prime factors of $n.$ $$\square$$
Proposition-6 means once we calculate all $1$-centrifuge admissible values of $k$ for a given $n$ using Sivek’s Main Theorem, we can find all possible sums of these $k$ to get all the $2$-centrifuge admissible $k.$ However, we wished to further characterize the set of all $2$-centrifuge admissible $k.$
Before continuing, we introduce a classical theorem that will aid in the characterization.
Sylvester’s Theorem #
Theorem-3#
Given positive coprime integers $p$ and $q$, we can express any integer $t\geq (p-1)(q-1)$ as $t = ap+bq$ where $a,b \in \mathbb{N}\cup{0}.$
Initial Bound Characterizing $2$-Centrifuge Admissible $k$ #
Consider the data for $n=21:$
2-centrifuge admissible: {0, 3, 6, 7, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 32, 33, 35, 36, 39, 42}
Sums of prime factors of 21: {0, 3, 6, 7, 9, 10, 12, 13, 14, 15, 16, 17...} (All integers greater than $11$ follow by Sylvester’s Theorem)
Looking at the numerical data, we can observe that for $k\leq n$, the two sets are the same.
Proposition-7#
Let
Proof: For any
First, we consider the case when $n = p^{\alpha}$ for some prime $p.$ Suppose $k \in S.$ Since $p$ is the only prime factor, we have $k = ap \leq n$ for some $a\in \mathbb{N}\cup {0}.$ Then, by Sivek’s Main Theorem, it holds that $k$ itself is $1$-centrifuge admissible, so we can balance $k$ in the first centrifuge and none in the second.
Now, suppose $n=pq$ for two distinct primes $p$ and $q.$ Suppose $k \in S.$ This means that $k = ap+bq$ for $a, b \in \mathbb{N}\cup {0}$ and $k\leq n.$ Note that if $k=n,$ then we can place all the vials in the first centrifuge (which would be balanced) and none in the second centrifuge. So, now we consider $k < n = pq.$ This means that $ap<n$ and $bq<n$. Thus, we can split $k$ over two centrifuges. First, we place $k_1 = ap$ vials in the first centrifuges. Then, we place $k_2 = bq$ vials in the second. By Proposition-5, these $ap$ and $bq$ are $1$-centrifuge admissible.
Finally, consider $n = pqm,$ where $p$ and $q$ are the two smallest prime factors of $n,$ and $m$ is the product of the remaining factors. By the two other cases, we can assume that $m\geq 2.$ Now, we consider cases for $k \in S$ and show that $k$ is $2$-centrifuge admissible.
First, consider
Next, we consider the case where
Improved Bound #
In the previous section, we showed that with two centrifuges, $k$ being expressible as a linear combination of prime factors of $n$ is equivalent to the problem of expressing $k$ as the sum of some $k_1, k_2$ such that $k_1$ and $k_2$ are both $1$ centrifuge admissible for all $k\leq n$. We now improve the upper bound of $k$ for which the statement holds. This is important for our generalizations beyond $2$ centrifuges.
By experimentation, we come up with the following proposition.
Proposition-8#
Let
Proof: Let $n=pqm$ where $p,q$ are the smallest two distinct prime factors of $n$. We know that $S=T$ for all $k\leq n$ by Proposition-7. So, we are only left to prove the proposition for the case when $n < k \leq 2n - (p-1)(q-1)$.
By Sylvester’s Theorem, we know that
Thus, to establish the equality of $S$ and $T$ for a range with lower bound greater than $n$, it is both necessary and sufficient to check if the integers in that range are elements of $T$.
Lemma-1#
If $k\in T$, then $2n-k \in T$1.
Proof: If $k\in T$, we have $k = k_1+k_2$ where $k_1, k_2$ are $1$-centrifuge admissible, then
By the above lemma, if
Since, $2n-k < n$, we have
Thus, we have proven that for all
On pondering whether we can improve the bound for $k$ further, we find a counterexample. Consider $n=21$. We cannot express $31$ as $k_1 + k_2$ where $k_1$ and $k_2$ are $1$-centrifuge admissible. However, $31. = 4\cdot 7 + 1\cdot 3$. Hence, we cannot necessarily say $k$ is $2$-centrifuge admissible if and only if it is a sum of prime factors of $n$ for any $k\geq 31$. $31 = 42 - 11 = 42 - (3-1)(7-1) + 1$. We can generalize such a counterexample to show that we cannot further generally extend the bound.
Allowing Mass of Two #
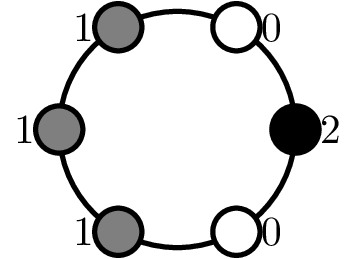
Another question we can consider is the following: what $k$ are balanced over a centrifuge with $n$ spots if we allow vials to have masses 0 (nothing placed there), 1 or 2, where $k$ represents the total mass of the vials. In the context of sums of roots of unity, this corresponds to allowing repeating a root of unity at most two times. For instance, consider the following balanced configuration with $n=6$ and $k=5.$
For a given $n,$ say $k$ is “$r$-mass admissible” if a centrifuge can be balanced with a mass from $0$ to $r$ in each slot.
For example, in the example given above, we would say for $n=6,$ $k=5$ is $2$-mass admissible.
Superposition #
Proposition-9#
For a given $n$, $k$ is 2-centrifuge admissible implies $k$ is 2-mass admissible.
Proof: As discussed in the previous section (Two Centrifuges), if $k$ is $2$-centrifuge admissible, then $k = k_1 + k_2,$ where $k_1$ and $k_2$ are $1$-centrifuge admissible (individually balanced). This means that we can superimpose the two centrifuges on top of each other. For instance, if in position $i,$ there is one vial in the first centrifuge and one vial in the second centrifuge, we can combine those to be a vial of mass $2.$ This will be balanced since it is the sum of two balanced configurations. Note that since we are superimposing only $2$ centrifuges, we will never end up with a mass greater than $2.$ $$\square$$
Now, before continuing, we introduce a generalized version of the Complement Principle for arbitrary masses.
Consider a configuration of masses $0$ to $r$ (no vial is considered mass $0$). Then, the complement of the configuration is obtained by replacing a mass $m$ with mass $r-m.$
For instance, the example below shows a configuration that is $2$-mass admissible and its complement, which is also $2$-mass admissible.
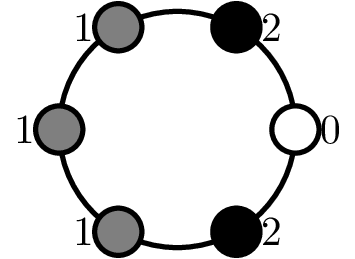

Complement Principle - Generalized for arbitrary masses #
Proposition-10#
A configuration is balanced if and only if its complement is balanced.
Proof: Suppose we are considering $r$-mass admissible numbers. Then, we know that a full centrifuge corresponds to $r (\zeta_n^{0} + \zeta_n^{1} + \zeta_n^{2}+\cdots + \zeta_n^{n-1}) = 0.$ Suppose we have some $n$-th roots of unity that sum to zero:
Based on our explorations, we conjectured that the converse was also true: any $k$ that is $2$-mass balancing is $2-$ centrifuge balancing. First, we considered $k\leq n.$
Proposition-11#
For $k\leq n$, if $k$ is $2$-mass admissible, then $k$ is $2$-centrifuge admissible.
Proof: Limiting repetition of roots of unity to twice is a subset of allowing any number of repetitions. So, by Lam and Leung’s Main Theorem, it follows that if $k$ is $2$-mass admissible, then $k$ is a sum of prime factors of $n.$ Since $k \leq n$, Proposition-7 implies that $k$ is two centrifuge admissible. (Note that this combined with Proposition-9 implies that the problem of masses 0, 1, and 2 is equivalent to the problem with two centrifuges for $k\leq n.$) $$\square$$
The below figure summarizes the proof strategy.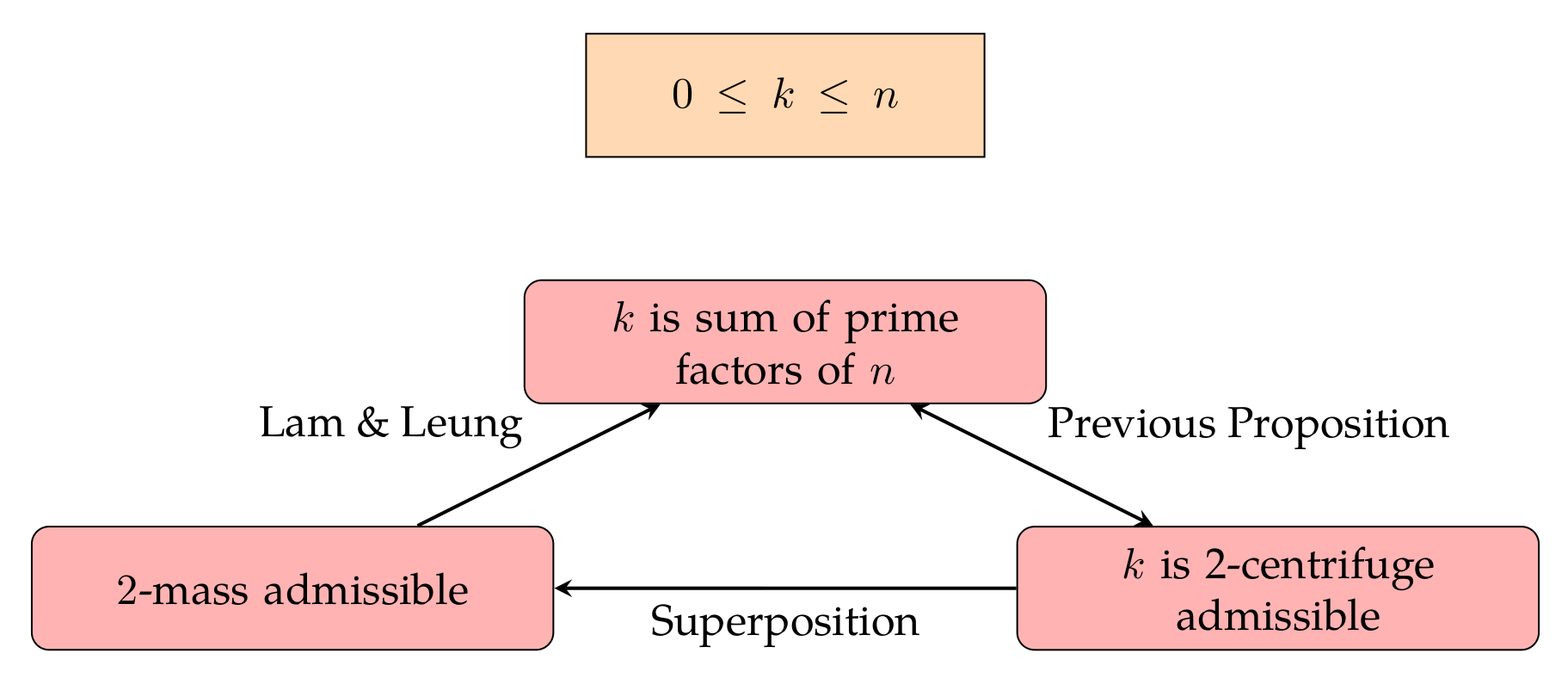
Note that we can use a similar proof strategy when generalizing (albeit with slightly different bounds and cases).
In fact, the connection between $2$-mass admissible and $2$-centrifuge admissible holds for $k>n$ too. However, we lose the intermediate connection of linear combinations, as shown in the above figure. For instance, for $n = 6,$ $k = 11,$ $11 = 3+3+3+2,$ but with some experimentation, we note that $11$ is neither $2$-centrifuge admissible nor $2$-mass admissible. However, the connection between $2$-centrifuge admissible and $2$-mass admissible still holds.
Proposition-12#
For $k>n,$ if $k$ is $2$-mass admissible, then it is $2$-centrifuge admissible.
Proof: Consider a $k>n$ such that $k$ is $2$-mass admissible. Now, consider the complement of such a configuration, which will also be balanced. Also, note that the complement will have $2n-k<n$ total mass. This means that $(2n-k)$ is $2$-centrifuge admissible, as we proved in Proposition-11. Now, we consider what this means in the context of the roots of unity. Let $S_k$ be the original sum for $k>n.$ Then, by Proposition-10, the complementary sum, say $S_{2n-k}$ satisfies
So, we can see that
For example, consider $k=10$ when $n=6$.
More Than Two Centrifuges #
Proposition-13#
For a given $n,$ the set of all $r$-centrifuge admissible $k$ is given by
Proof: By definition, if $k$ is $r$-centrifuge admissible, then it can be balanced over $r$ centrifuges. This means that each centrifuge is balanced. Thus, we can consider $k_1, \cdots k_r$ for each centrifuge, and we need each to be balanced, so we must have the restriction that $k_i$ is $1$-centrifuge admissible.
Conversely, suppose we have $k_i$’s that are each $1$-centrifuge admissible. Then, by definition, the sum $\sum_{i = 1}^r k_i$ is $r$-centrifuge admissible since we are summing $r$ different $1$-centrifuge admissible values. $$\square$$
Let the number of centrifuges be $r$. Then, define
Proposition-14#
$T \subseteq S$.
Proof: This is a generalization of the Superposition Principle in Proposition-9. Consider $r$ centrifuges such that each centrifuge is balanced. We can superimpose each centrifuge on to each other where if $y$ of the $r$ centrifuges have a vial in a certain position, we replace it with a vial of mass $y.$ Note that this will be balanced since the sum of vanishing sums of roots of unity is always vanishing. Also, we will never have mass greater than $r$ since $y\leq r.$ $$\square$$
Proposition-15#
$S \subseteq T$.
Proof: First, we prove this for
Base Case: $r = 2$. Follows by Proposition-8. Inductive Step: Consider the case when $n=pqm$ where $m\geq 2$ first.
Suppose all $k$ such that
Moreover, if we add a full centrifuge, then all $k$ such that
We present two proofs for the $n=pq$ case.
Proof 1: #
Base case: The base case is the same as before. Inductive Hypothesis: The problem in the $pq$ case arises in the fact that for $n=pq$, we may have
Taking the difference of the upper and lower bounds of the range, we get $2(p-1)(q-1) - n$. Since this difference is greater than $p$ (apart from in a few cases as considered later) we have by the pigeon hole principal that there exists at least one multiple of $p$ in the range. Also, the range lies between $0$ to $n$. Thus, there exists some $k_2$ that is $1$-centrifuge admissible.
Now, we consider the cases when
Proof 2: #
We are working with the same gap as before, but here we first note that once we close the gap for $r=2$ to $r=3$, we will be able to employ the same proof as for $n=pqm$ with only $r\geq3$ instead. Then, we can’t necessarily have
Now, we prove this for
We now have one last case to deal with, that is when $n= p^\alpha$. Since the only values of $k$ that are $1$-centrifuge admissible in this case, and the set of multiples of $p$ is closed under addition, the only values of $k$ that are $r$ centrifuge admissible in general are the multiples of $p$. The theorem thus follows.
Theorem-4#
$S = T$
Proof: We know that $S\subseteq T$ and that $T\subseteq S$. Hence, $T=S$. $$\square$$
Theorem-5#
For a given $n,$ $k$ is $r$-mass admissible if and only if $k$ is $r$-centrifuge admissible.
Proof: By Proposition-14, any $k$ that is $r$-centrifuge admissible is also $r$-mass admissible. By Lam & Leung’s Main Theorem, any balanced configuration of masses from $1$ to $r$ must have $k$ be a sum of prime factors of $n.$ For
Finally, we consider the case for
Number of Balancing Constructions #
In this section, we explore the number of constructions we can construct so as to balance a centrifuge with $k$ vials and $n$ spots. This is equivalent to finding the number of combinations of $k$ $n$-th roots of unity that have a vanishing sum (sum to $0$).
Yet again, we first do so for simpler cases, such as when $n$ is a prime power and a product of two distinct primes.
Proposition-16#
For a given pair $(n,k)$, where $n=p^\alpha$ for some prime $p$ and natural number $\alpha$, we have
Proof: By Lam and Leung, we know that in order to have a vanishing sum with $k$ terms, when $n$ is of the form $p^\alpha q^\beta$, we have only two minimal vanishing sums (up to rotation), namely the $p$-th roots of unity and the $q$-th roots of unity. In our context, this means that we must construct balanced configurations only out of groups of $p$ or $q$ equally spaced vials. In our case $\beta = 0$, so $k$ must be a multiple of $p$ (as we are using groups of the $p$-th roots of unity. Hence, we confirm that $k/p \in \mathbb{Z}$ Moreover, given a $k$, there exist $k/p$ groups of $p$ equally spaced $n$-th roots of unity that each sum to $0$. Thus, we are choosing $k/p$ sets of $p$ equally spaced $n$-th roots of unity from all possible $p$ equally spaced $n$-th roots of unity.
So our problem becomes finding the number of ways to choose $k/p$ groups of $p$ equally spaced $n$-th roots of unity we can find that sum to $0$.
Now, we have $n$ ways to choose the first among $p$ $n$-th roots of unity. The remaining $p-1$ vials of that group are fixed since they must be equidistant.
However, since there are $p$ vials per group, we are over-counting $p$ times. Thus, we must divide by $p$.
So, we have a total $n/p$ groups of $p$ equally spaced $n$-th of unity to choose from. From these, we must choose $k/p$ to get a configuration with $k$ groups. This can be done in
We may use a similar strategy to prove the result in the case when $n=pq$ for distinct primes $p$ and $q$. Thus, we come up with the following proposition:
Proposition-17#
If $n=pq$, there are $\binom{n/r}{k/r}$ possible ways to balance $k$ centrifuges, $k \leq n$ where $r\in {p, q}$ and $r|k$.
Proof: First, we note that by Proposition-4, either $p|k$ or $q|k$. Without loss of generality, we assume $p|k.$ Furthermore, we can write $k$ as a sum of $p$’s and $q$’s in only one way, $k = ap$, $a \in \mathbb{N}$ (as we are considering $k \leq pq$, and as such, we can not substitute $q$ $p$ terms in the sum with $p$ $q$ terms, as $a \leq q$, with the exception of $k = n$, where we can note that the two methods are an identical and complete use of the $n$-th roots of unity). In all other cases, we can disregard $q$, and instead focus on how to place $a$ rotations of the $p$-th roots of unity. We note that there are $\frac{n}{p}$ distinct rotations, and we choose $a = \frac{k}{p}$ of them, implying
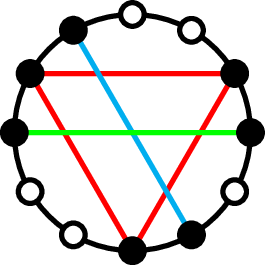
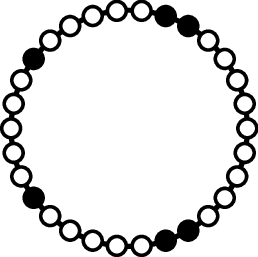
For $n$ more complicated than $n = pq$, this gets more complicated. If $n = p^{\alpha}q^{\beta}$, there may be methods to count using inclusion-exclusion principles, even as we start having different combinations with which to balance, such as $8 = 2+3+3 = 2+2+2+2$ for $n=18$. However, we did not manage to find a general formula, as we ran out of time - this is an area of future interest. In addition, if $n$ is factored into three or more distinct primes, we end up losing the ability to assume a decomposition into equally spaced sets of minimal vanishing sums. Lam and Leung give a method of constructing asymmetric minimal vanishing sums in the $n$-th roots of unity, as shown below for $n=30=2\cdot3\cdot5$
Total Number of Vanishing Sums #
While it is difficult to find the number of vanishing sums with $k$ $n$th roots of unity for a given $k, n$, it might be simpler to find the total number of vanishing sums over all possible values of $k$ given an $n$. Let this be represented by $K_n$
We start with the case when $n=pq$ where $p$ and $q$ are primes.
Future Questions #
We have a number of unanswered questions and projects that we were unable to even begin in our brief time at PROMYS. Notably, there is the possibility of a formula for counting balanced arrangements, which we believe to be very possible for $n = p^{\alpha}q^{\beta}$, and substantially more difficult for generalized $n$, for the reasons discussed above. Another question is to find a non-exponential time algorithm to balance a centrifuge, for given $k$ and $n$. Looking to Lam and Leung’s paper, in addition to the one we used that worked in the complex numbers, they have one proving an equivalent statement for finite fields, but we are unaware of an equivalent of Sivek’s work in the case of finite fields, and considered attempting a proof in finite fields of an analog to his theorem. There are also interesting questions as to vanishing sums of cosines, and how equivalent to vanishing sums in roots of unity they are, through Euler’s Identity.
We will see more about this lemma in a more formalized way in the form of a generalized Complement Principle later in this paper ↩︎